Prof Kamran Behnia (ESPCI- Paris, FRANCE) gives a webinar on ‘How heat propagates in normal liquid 3He’ (4PM UK time)

Join Zoom Meeting

here

Meeting ID: 871 8387 3228 Passcode: 767885

One tap mobile +17193594580,,87183873228# US +12532050468,,87183873228# US

Join instructions https://us02web.zoom.us/meetings/87183873228/invitations?signature=WPzK9JbXBk5L3Tmc-qUiODuNe3xsT-8wn8e16CSw40c

Abstract

Landau’s theory of Fermi liquids was inspired by the case of liquid 3He. Thermal conductivity of 3He [1] conforms to this theory but contrary to a common belief, only at very low temperatures. The deviation from the expected temperature dependence can be explained by assuming that Landau’s quasi-particles are not the only players and there is another contribution to heat transport by a collective sound mode [2]. In the hydrodynamic limit when the scattering rate is larger than frequency, the celebrated zero sound [3] cannot be distinguished from the first sound. The empirical expression for this second channel of heat transport looks like a quantum version of the Bridgman equation for thermal conductivity of classical liquids [4]. A collective mode may also be relevant to transport in strongly correlated metallic Fermi liquids whose resistivity deviates from a quadratic behavior well below the Fermi degeneracy temperature.

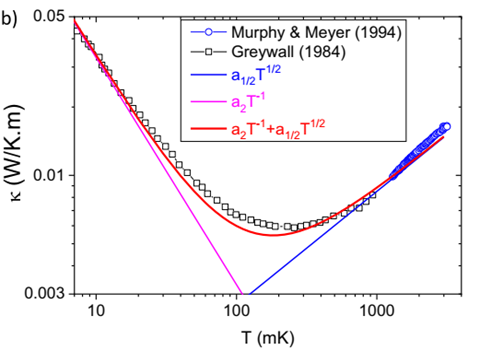
Figure 1: Thermal conductivity, κ, of liquid 3He as reported by Greywall (at zero pressure) and by Murphy and Meyer (at saturated vapor pressure). At very low temperatures (T ~ 0.01 K) in the Fermi liquid regime, κ ∝ T -1 (purple line). Above 0.5 K, κ ∝ T1/2. The red solid line represents a fit to the experimental data in the whole temperature range assuming that κ consists of the sum of the two terms.


[1] D. S. Greywall, Phys. Rev. B 29, 4933 (1984).

[2] K. Behnia & K. Trachenko, Nature Commun. 15, 1771 (2024).

[3] F. Albergamo et al., Phys. Rev. Lett. 99, 205301 (2007).

[4] P. W. Bridgman, P. W. Proc. Am. Acad. Arts Sci. 59, 141–169 (1923).